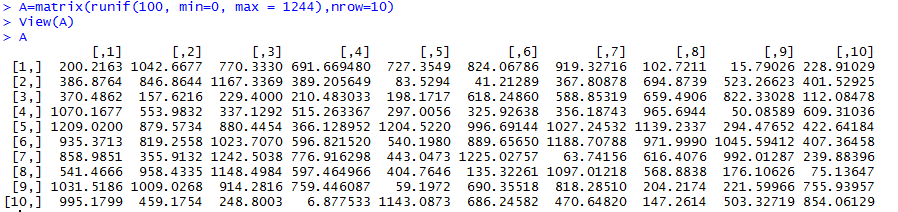
First, I created matrix A by randomly generating 100 numbers with the values between 0 and 100 and with 10 rows to make it square. It’s been ages since I’ve dealt with matrices, so I had to refamiliarize myself with how basic math functions work with them.
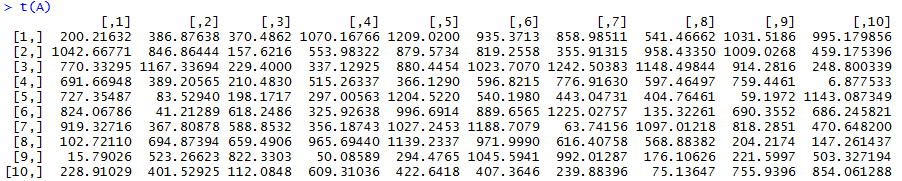
The transpose of A flips the values across the diagonal that connects [1,1] to [10,10] and is easily made with 4 short character strokes:
Next, I tried to create a randomized vector with > a=c(runif(10, min=0, max = 1244),nrow=10), but it ended up not working out, so I just made a numerically sequential vector with >a = c(1:10) to multiply with A. Each row of elements in the matrix are multiplied by the corresponding row in the vector.

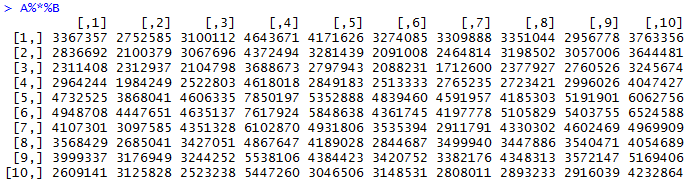
I multiplied matrix A with matrix B, which was made in the same randomized manner as matrix A:
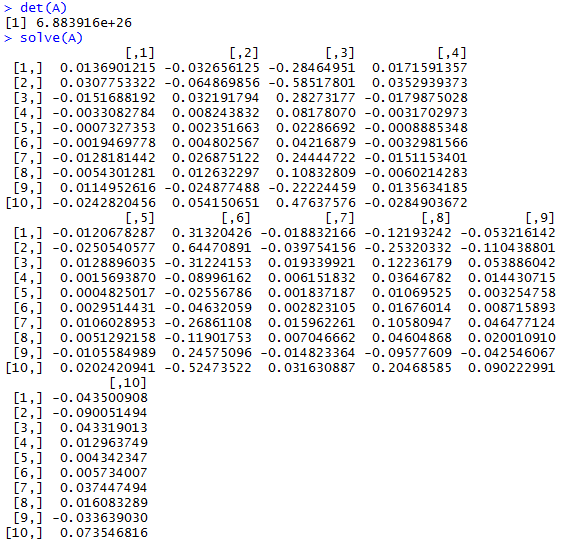
We test the determinate of A to make sure it is inverseable and, in turn, solvable. > det(A) gives us a non-zero value, which gives us a green light to run > solve(A) and find the inverse of A.