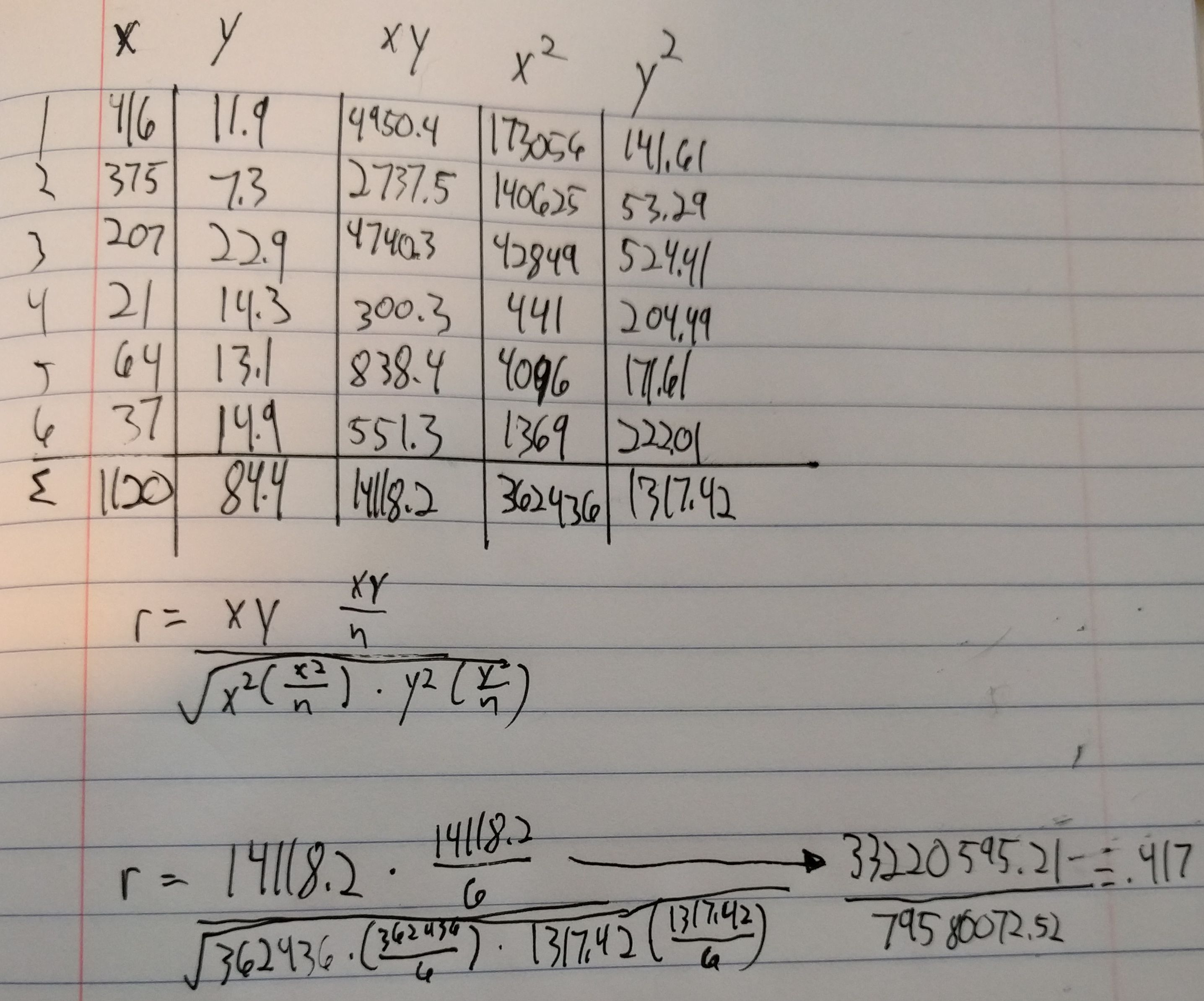by Ryan | Oct 2, 2016 | advanced statistics
A
Import vector of values of ice cream purchase numbers
>a <- c(8, 14, 16, 10, 11)
Generate random sample of 2 values and save to a vector
> b <- sample(a,2)
[1] 10 11
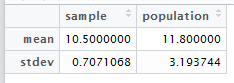
Calculate mean and standard deviation of the sample.
>mean(b)
[1] 10.5
> sd(b)
[1] 0.7071068
Create data.frame out of mean and stdev for the sample and population.
mean(a)
[1] 11.8
> sd(a)
[1] 3.193744
smp <- c(10.5,0.7071068)
> pop <- c(11.8,3.193744)
> c <- data.frame < (smp, pop)
B
- I think that the sample proportion will have the approximately the same distribution since nq = 5.
- I think 100 is the smallest value of n for which p is approximately normal because anything smaller than n = 100 will make np < 5. The high value of p is very limiting.
by Ryan | Sep 11, 2016 | advanced statistics
Initially, I was just going to calculate the correlation coefficient manually in R without using the functions, but then I decided that if I was going to do it manually then I may as well do it by hand. I ended up making a mistake with spacing by not thinking about how many digits would be made out of squaring an already triple digit number.
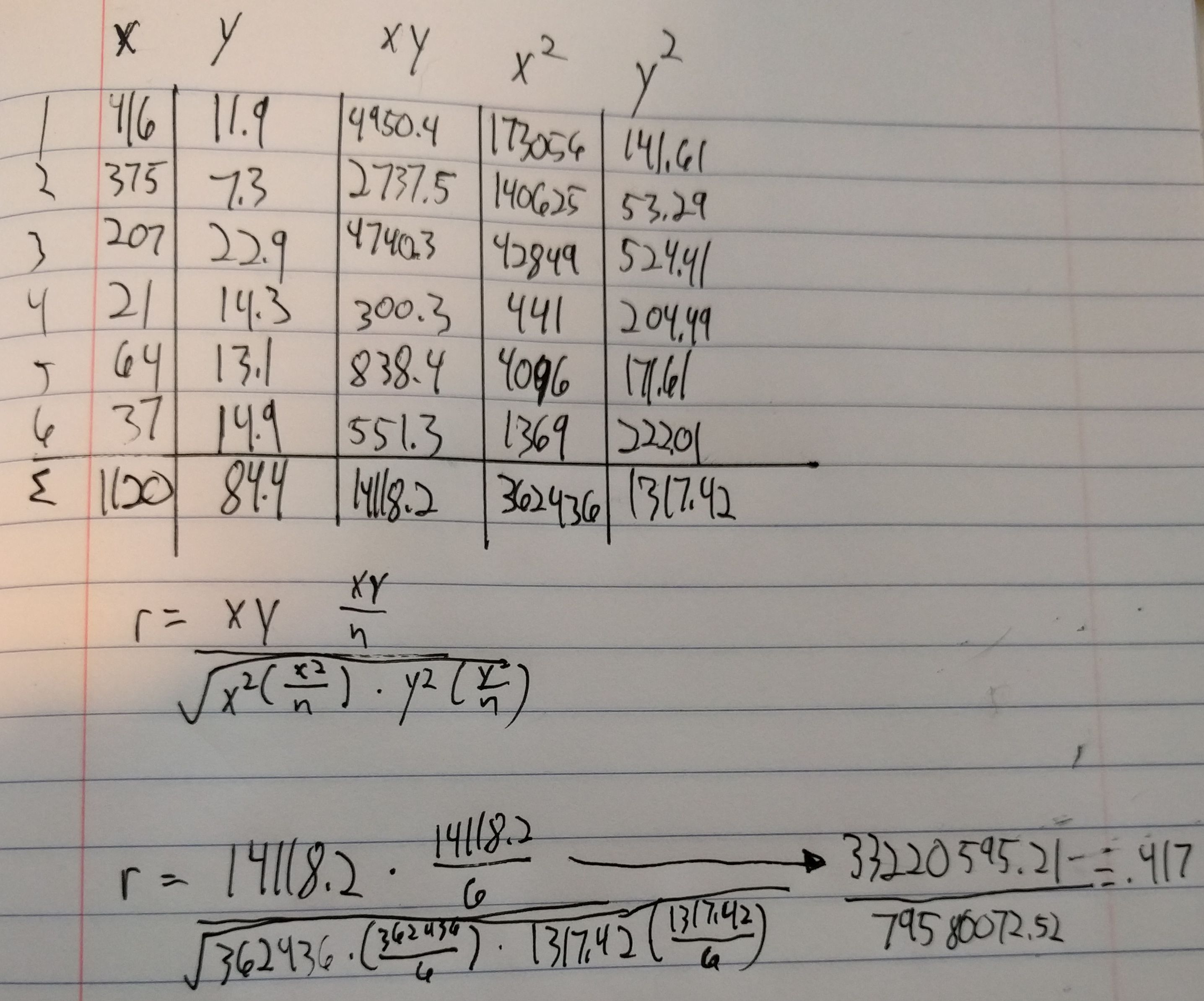
From there, inputting the x and y values into R and executing the cor.tests() were very simple and straightforward. I feel like I’ve gotten to the point with R where I don’t feel like I’m completely lost all the time.


by Ryan | Sep 5, 2016 | advanced statistics
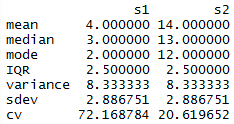
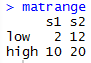
For this assignment, I decided to to make everything as one script and use the Source with Echo command to run it all at once. The only issue I had is that mode() does not yield a mode. It returns what storage mode the object uses, so I had to look up how to make a function to calculate the mode.
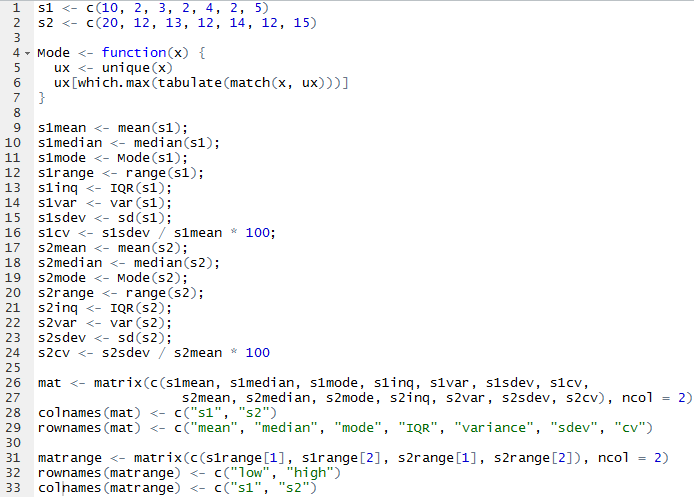
From there, I was able to call mat and matrange to pull up the tables of all the values.
by Ryan | Aug 22, 2016 | advanced statistics
ffff